Gravitation? Gibt’s doch gar nicht!

Die Flache Erde gehört zu den prominentesten und gleichzeitig irrsinnigsten Vertretern einer Gattung namens „Verschwörungstheorie“. Eine der beliebtesten Behauptungen: Gravitation würde es nicht geben. Wirklich nicht? In Folge 1 zum Themenkomplex „Schwurbelunsinn“ geht es um das, was uns auf der Erde hält. Und was wir brauchen, um davon los zu kommen. Eine Kolumne von Christian Unger

Bild von skeeze auf Pixabay

Was fällt schneller auf den Boden? Ein Hammer oder eine Feder? Nun, das kommt ganz auf die Umstände an. Im luftleeren Raum ist die Antwort… Halt! Ganz ohne Formeln werden Sie hier nicht auskommen, liebe Leserinnen und Leser, aber ich werde versuchen, es möglichst einfach und verständlich zu halten.

Gravitation ist die Kraft, die zwei Massen zueinander zieht. Ein sehr schweres Objekt – beispielsweise der Jupiter – zieht einen Satelliten mit derselben Kraft an wie der Satellit den Jupiter. Allerdings interessiert es den Gasriesen eben weit weniger, weil er eben weit größer und schwerer ist. Umso größer die Distanz ist, umso schwächer ist die Gravitation.
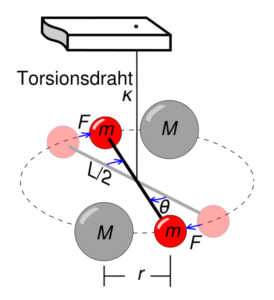
Um unsere Formel zu entwickeln, benötigen wir also zunächst die beiden zueinander in Wechselwirkung stehenden Massen (M1, M2) und deren Abstand zueinander, genauer genommen der Abstand der beiden Schwerepunkte (r). Die Einheit für die Kraft ist kg * m / s², auch Newton genannt. 1 Newton (1 N) entspricht dabei 1 kg * m / s². Wie man sieht, fehlt uns also etwas in unserer Variablensammlung.. Wo bekommen wir die Quadratsekunden her? Im Gegensatz zu vielen physikalischen Grundideen stand hierbei das Experiment vor den mathematischen Berechnungen. Isaac Newton hatte zwar bereits erkannt, dass es Gravitation gibt und dass sie von den jeweiligen Massen und der Entfernung abhängt. Er definierte diese allerdings nicht in einer schönen Formel, sondern nur als Verhältnisdefinition. Die Geburt der Gravitationskonstante Der erste Nachweis der Gravitationskonstante gelang Henry Cavendish im Jahr 1798. Dazu nutzte er folgende Versuchsanordnung:

Quelle: https://commons.wikimedia.org/wiki/File:Cavendish_Torsion_Balance_Diagram_de.svg

An einem Torsionsdraht, der alle horizontalen Drehbewegungen erlaubt, wird eine feste Stange befestigt, an deren Enden zwei gleichgroße Massen (m und m‘) befestigt werden. Im Abstand r dazu werden zwei deutlich größere, ebenfalls gleichgroße Massen (M und M‘) gestellt. Da sich die nahe einander befindlichen Massen anziehen, drehen sich m und m‘ jeweils zu M und M‘. Die Kraft F, die sie für die Strecke benötigten, konnte daraus abgeleitet werden, wobei natürlich Daten wie die Torsionssteifigkeit des Drahtes beachtet werden mussten.
Da die Bewegung von m und m‘ zu M und M‘ eine Beschleunigung darstellt, kommt auch das Quadratsekunden zustande. Kraft ist nichts anderes als Masse * Beschleunigung. Entwickelt man nun mit allen Variablen eine Formel und setzt die experimentellen Messergebnisse ein, kann man davon die Gravitationskonstante bestimmen. Dank Laser und Co. wurde diese Messung immer weiter präzisiert, wobei es insgesamt immer noch eine relativ große Ungewissheit ab der dritten Nachkommastelle gibt. Ich nutze:

Gravitationskonstante G = 6,672 * 10-11 m³ / (kg * s²)

In einigen Publikationen findet man auch abweichende Konstanten, die aber ebenso gut genutzt werden können.

Was nützt uns die Gravitation?

Das Experiment kann jeder einfach nachstellen. Er oder sie sollte dabei allerdings darauf achten, dass andere Einflüsse wie Windbewegungen möglichst ausgeschlossen werden. Die Stange mit den beiden Massen m und m‘ wird deswegen zumindest im wissenschaftlichen Umfeld in einem Kasten aufgebaut, der solche Einflüsse verhindert. Für den Nachweis zuhause, in der Schule oder beim Club der Schwurbelidioten e.V. reicht aber auch der o.g. Versuchsaufbau und etwas Geduld aus. Für die meisten Verschwörungstheoretiker wird es bereits dort schwierig, mit ihren abstrusen Ideen die Gravitation wegzureden.

Die Gravitation ist sehr klein. Im Bereich der Teilchen ist sie sogar so klein, dass sie zu vernachlässigen ist. Elektromagnetische Kraft sowie die schwache und starke Wechselwirkung sind für Teilchenphysiker deutlich relevanter, weshalb die Gravitation dort meist nur ein Schulterzucken auslöst.

Dennoch ist die Gravitation überlebensnotwendig. Sterne entstehen wie Planeten erst durch die Gravitation und die Erde dreht nur dank Gravitation seit Jahrmilliarden ihre Runden um unseren wichtigen Energielieferanten. Wir bleiben erst durch die Gravitation auf der Erde „kleben“. Dabei ist sie allerdings nicht so groß, dass unsere Muskelkraft Probleme hat, die Gravitation bis zu einem gewissen Punkt zu überwinden. Wir können uns bewegen, sogar bis zu einer gewissen Höhe springen und selbst an großen Objekten bleiben wir nicht hängen. Eine 80 KG schwerer Person und ein 50 KG schwerer Mensch ziehen sich beispielsweise mit 0,00000006672 N an. Der Mensch merkt diese sehr geringe Kraft einfach nicht.

Schwerelos durch das All

Atemlos durch die… Entschuldigung, mit so etwas wollte ich Sie sicherlich nicht langweilen, liebe Leserinnen und Leser. Stattdessen möchte ich über einen Mythos aufklären, der in der Gesellschaft weit verbreitet ist: Die Schwerelosigkeit im All. Bereits auf der ISS solle diese herrschen, wenn es nach vielen Menschen in Deutschland, aber auch anderswo, geht.
Das ist aber erstmal eine logische Aufgabe: Warum soll in der ISS in ca. 410 KM Höhe Schwerelosigkeit herrschen, wenn in der zehnfachen Entfernung noch der Mond von der Schwerelosigkeit unseres Planeten festgehalten wird? Vereinen wir unsere bereits bekannten Variablen bzw. die eine Konstante zu einer Formel, erhalten wir:
F = G * M1 * M2 / r²
Bezogen auf eine Person mit einem Gewicht von 80 KG auf der ISS würde das bedeuten:
F = 6,672 * 10-11 m³ * kg-1 * s-2 * 5,972 × 1024 kg * 80 kg / (6,78 * 106 m)
Hierbei ist der Taschenrechner explizit erlaubt. Wir kommen dann auf:
F = 693.43 N.
Auf der Erde können wir eine kleine Rechenerleichterung nutzen. Die Erdbeschleunigung beträgt auf Normalnull etwa 9,81 m / s², was wir einfach mit dem Gewicht eines Menschen multiplizieren können. Wir kommen dann also auf:
F = 784,8 N.
Wie wir sehen, unterscheiden sich beide Zahlen nicht sonderlich voneinander. Die Anziehung der Erde auf die ISS und den dort befindlichen Astronauten beträgt etwa 88,4 % der Erdanziehung auf der Oberfläche. Wie wir an der Formel sehen, besitzt die Gravitation keine Grenze. Sie ist grundsätzlich unendlich weit wirksam. Selbst in einer Millionen Lichtjahre Entfernung besitzt die Erde noch eine Anziehungskraft, auch wenn diese natürlich verschwindet gering ist. Wer Lust hat, kann das ja mal ausrechnen.

Warum sind die Astronauten auf der ISS dann scheinbar schwerelos?

Eine – leider auch von einigen Astronauten und Physikern – vorgebrachte Erklärung liegt in der Fliehkraft. Die Fliehkraft würde die Gravitation ausgleichen. Das ist zwar nicht verkehrt, aber eben keine Erklärung, warum Alexander Gerst und Co. ihr schwebendes Frühstück mit dem Mund einfangen konnten und können. Die Fliehkraft ist nur eine Scheinkraft, die Gegenkraft zur Gravitation. Wir rechnen auch hier.
Die Fliehkraft berechnet sich mit F = M2 * v² / r, wobei M2 die Masse des leichteren Objekts, v die Geschwindigkeit und r die Distanz zwischen dem Mittelpunkt und der Kreisbahn ist, die de facto gleich dem r aus der Gravitationsberechnung ist. Für eine stabile Umlaufbahn setzen wir beides gleich:
FGr = FFl, also G * M1 * M2 / r² = M2 * v² / r
Wir multiplizieren das ganze mit r, wodurch wir schon mal eine Variable auf der rechten Seite streichen können. Ebenfalls können wir beide Seiten durch M2 teilen, womit die Masse des leichteren Objekts, welches eine Kreisbewegung um das schwerere Objekt macht, ebenfalls irrelevant wird. Da eine Geschwindigkeit am besten ohne Quadrat verständlich ist, ziehen wir noch die Wurzel. Wir erhalten dann also: √∗/=
Wenn wir also wissen wollen, wie schnell die ISS fliegen muss, um eine stabile Umlaufbahn zu haben, müssen wir hier nur unsere bekannten Werte einfügen. Wir erhalten:
v = 7,55 km / s
Angegeben ist die Geschwindigkeit der ISS übrigens mit 7,6 km/s. Ein bisschen ungenau sind unsere Zahlen also schon. Aber: Auch jedes andere Objekt, von einem Staubkorn über einen kleinen Satelliten bis zu einem potenziellen zweiten Mond mit vielfacher ISS-Masse müsste in dieser Höhe exakt diese Geschwindigkeit haben, um eine stabile Kreisbahn zu bekommen. Das sich Gravitation und Fliehkraft ausgleichen, liegt also an einem: Der Geschwindigkeit. Und die unterscheidet sich von der Beschleunigung.

Wie die ISS an der Erde vorbeifällt

Folgt man dem Gedanken weiter, wird klar, dass wir eigentlich keine Raumfahrt betreiben. Wir betreiben viel eher ein Raumfallen. Deshalb sind Astronauten auch scheinbar beim Flug von der Erde zum Mond schwerelos, wo es sehr schwer wird, der Fliehkraft die Schuld zu geben. Viel mehr werden die Astronauten in ihre Sitze gedrückt, solange eine Beschleunigung durch die Kraft der Raketen wirkt. Fällt dies weg, liegt keine Beschleunigung, sondern nur noch eine Geschwindigkeit vor. Die Astronauten befinden sich dann im freien Fall.
Dieses lässt sich ebenfalls gut experimentell nachweisen. Wer viel Adrenalin mag, einen Hersteller von Aufzügen kennt und Ordnungsamt bzw. Polizei von sich fernhalten kann, kann sich in einem Fahrstuhl nach unten fallen lassen. Er wird dort schwerelos werden. Nicht so illegal sind Parabelflügel. Ein Pilot fliegt hierbei steil nach oben und nimmt dann den Schub plötzlich weg. Das Flugzeug steigt noch ein Stück. Da keine Beschleunigung sondern nur noch eine Geschwindigkeit wirkt, werden die Personen noch während des Steigflugs schwerelos. Es fehlt die Beschleunigung, es herrscht nur noch eine Geschwindigkeit, die aber nicht so schnell ist, um von der Erde zu „flüchten“ und das Flugzeug fällt nach unten. Auch dort ist dann der freie Fall in Form einer scheinbaren Schwerelosigkeit zu spüren. Bei der ISS passiert dasselbe: Sie fällt. Sie fällt aber eben so schnell, dass sie an der Erde immer vorbei fällt. Würde die ISS plötzlich auf eine deutlich geringere Geschwindigkeit abgebremst werden, würden sie zur Erde fallen – und bis die armen Astronauten dort auftreffen, werden sie ebenfalls schwerelos sein.
Wem das alles zu viel Adrenalin ist, kann auch fallende Wassertropfen (diese können nur rund sein, wenn sie im freien Fall schwerelos sind) beobachten oder den Fallturm Bremen besuchen, der in seiner Größe in Europa einmalig ist. Während Forscher dort lange Wartezeiten in Kauf nehmen müssen, können Besucher einmal im Monat an einer Führung teilnehmen.

Wir flüchten von der Erde

Wollen wir von der Erde weg, benötigen wir einen richtig starken Antrieb. Es muss also eine Energie, also kg * m² / s², aufgebracht werden. Dennoch reden wir von einer Fluchtgeschwindigkeit. Eine Geschwindigkeit ist aber eben nicht m² / s², sondern eben m / s (oder, im Alltag, km / h). Wie verlieren wir hier also plötzlich unser Quadrat und wo kommt das kg her?
Auch hier setzen wir wieder Formeln gleich. Als erstes nehmen wir – keine Überraschung – wieder unsere Gravitationsformel F = G * M1 * M2 / r2. Da dies aber nur die Anziehung ist, also die Kraft, entspricht sie eben nicht der Energie, die aufgewendet werden muss, um von der Erde zu flüchten. Um eine von Kraft auf Energie zu schließen, müssen wir das ganze noch mit dem Weg multiplizieren, der überwunden werden muss. Da sich alles zum Mittelpunkt zieht, wäre dies wiederum der Erdmittelpunkt r. Wir bekommen also r * G * M1 * M2 / r2, gekürzt: G * M1 * M2 / r. Als Einheit ist dies m³ * kg-1 * s-2 * kg * kg * m-1. Wieder gekürzt und in eine standardisierte Form gebracht: kg * m² / s², alternativ Nm (Newtonmeter) oder J (Joule) und damit unsere Energie. Dagegen setzen wir die kinetische Energie, die aufgewendet werden muss. Die Gleichung sieht dann so aus:
G * M1 * M2 / r = ½ M2 * v²
Schon wieder – Überraschung, Überraschung! – streicht sich die kleinere Masse heraus. Auch für die Fluchtgeschwindigkeit ist es irrelevant, ob wir ein Staubkorn oder ein Raumschiff haben, auch wenn bei letzterem deutlich mehr Sprit benötigt wird, um die Geschwindigkeit zu erreichen. Wir multiplizieren das ganze außerdem mit 2 und ziehen die Wurzel, um wieder v für Geschwindigkeit zu bekommen:
2 * G * M1 / r = v, also:
Wurzel von (2 * 6,672 * 10-11 * 5,972 * 1024 / 6,37 * 106) = v, somit bekommen wir
v = 11184,93 m/s, also etwa 11,2 km/s. Wenig erstaunlich stimmt das mit dem überein, was NASA oder ESA auf ihren Webseiten als Fluchtgeschwindigkeit nennen.

Ist die Gravitation richtig gut erforscht?

Trotz Formeln – hier habe ich nur die einfachsten dargestellt – ist die Gravitation noch nicht vollständig erforscht. Ganz im Gegenteil. Denn wir wissen zwar, dass es sie gibt, wir können sie zweifelsfrei und für jeden durchführbar experimentell nachweisen. Doch warum es sie gibt, wissen wir nicht. Folgen wir dem Standardmodell der Teilchenphysik, bedarf jede Wechselwirkung auch ein Elementarteilchen, genau genommen ein Eichboson. Postuliert wird die Existenz von Gravitonen, die aber extrem leicht oder sogar masselos sein würden. Sie sind extrem schwach nachweisbar, da ihre Effekte eben auch so klein sind. Bisher haben wir keines gefunden.
Ist die Gravitation daher nicht nachgewiesen, wie so viele Flacherdler meinen? Dort wird beispielsweise in einem YouTube-Video behauptet, eine Masse Materie würde fallen, weil sie dieselbe Masse Luft verdrängt. Das wäre schwierig. Ein Kugelstoßer würde mit seiner 7,3 KG schweren Kugel also über 6 m³ Luft „einnehmen“. Mit was wird dann das restliche Volumen gefüllt? Ab und an hört man dann vom „Äther“. An deren Existenz kann man natürlich glauben, wenn man die letzten Jahrzehnte der Physik verschlafen hat, welche die Existenz dieses Äthers eindrucksvoll widerlegte. Im Äther kann man eben auch nicht atmen. Zudem würde es nicht erklären, warum – aus Sicht eines Menschen – immer alles nach unten fällt. Wenn es nur um die Masse geht, würde es auch nicht erklären, warum ich weniger Luft mit der Kugel verdrängen kann als Weltrekordhalter Randy Barnes. So scheint es doch nicht nur um das Gewicht zu gehen.
Die Gravitation gibt es also wirklich – und wir können alle dankbar darüber sein. Um die Eingangsfrage zu beantworten: Es fällt alles gleich schnell, zumindest im luftleeren Raum. Auf der Erde stört allerdings häufiger die Atmosphäre. Die leichte Feder reagiert eher auf den Luftwiderstand. Die Astronauten, die bei den Apollo-Missionen den Mond erreichten, haben dies mit einer Feder und einem Hammer dort aber praktisch nachgewiesen, wenn auch nur begrenzt unter wissenschaftlich einwandfreien Bedingungen. Auch wenn unsere Flacherdler das vermutlich genauso wenig akzeptieren werden. Waren die Amerikaner vielleicht nicht auf dem Mond? Immerhin können wir keine Sterne sehen und die Flagge weht auch, ohne dass es dort Wind gibt. Das riecht nach Folge 2 vom Schwurbelunsinn.